KEY Concept For Chpt. 8.1 Introduction to Trigonometry
The full meaning of word 'Trigonometry' is 'Measuring the three sides' of a triangle.
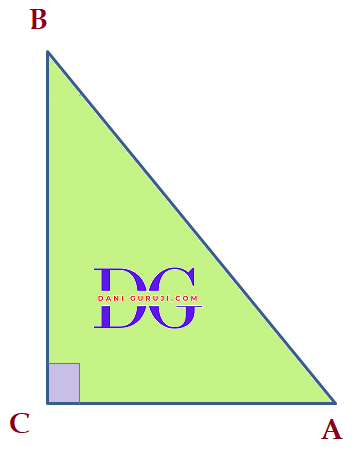
Right Angle Triangle
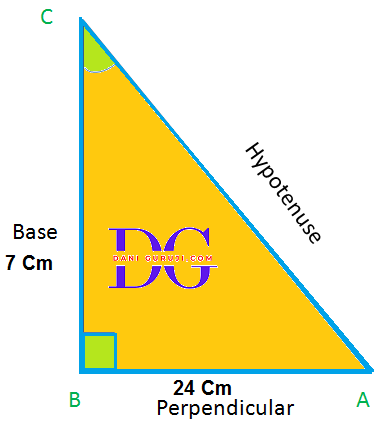
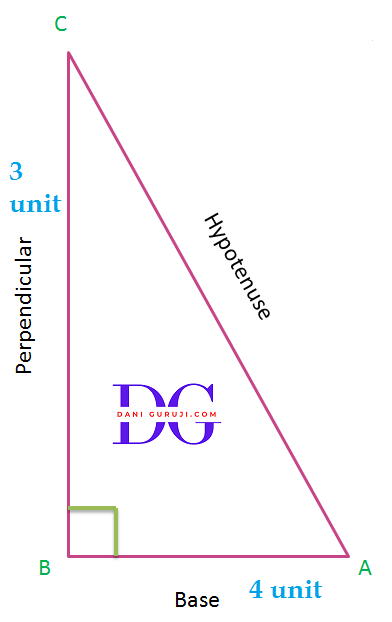
Right Angle Triangle, A triangle with an angle equal to 90° and there are two acute angles is called Right Angled Triangle
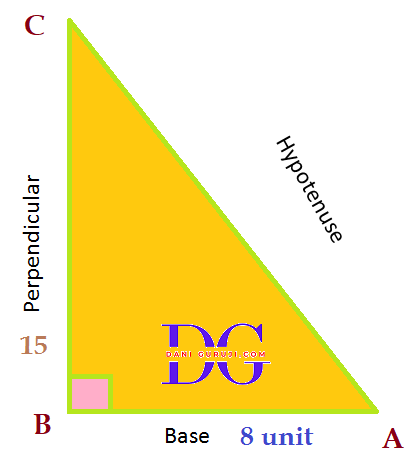
Hypotenuse
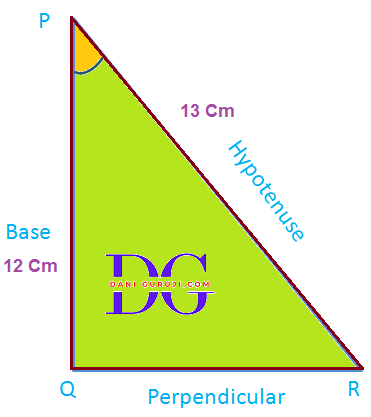
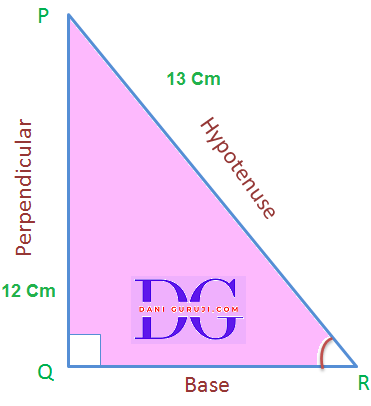
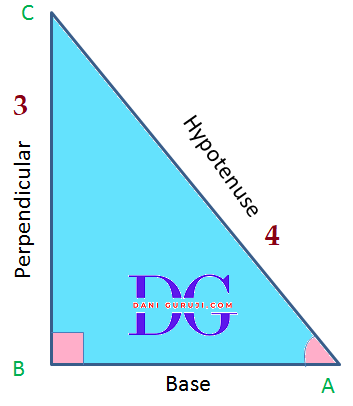
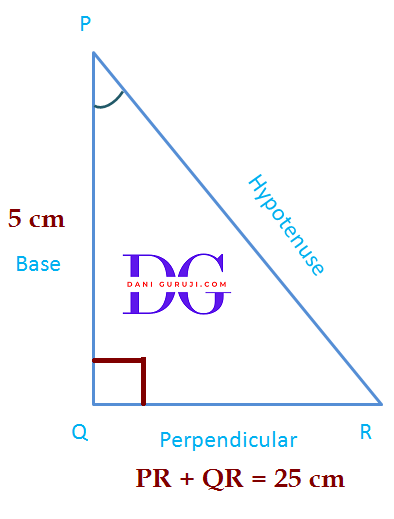
The side opposite to right angle ( 90°) is called Hypotenuse in a right angled triangle.
Base
The side adjacent to one of the acute angle, (say ∠A in the given below figure) is called Base.
Perpendicular
The side opposite to the acute angle, (say ∠A in the given below figure) is called Perpendicular.
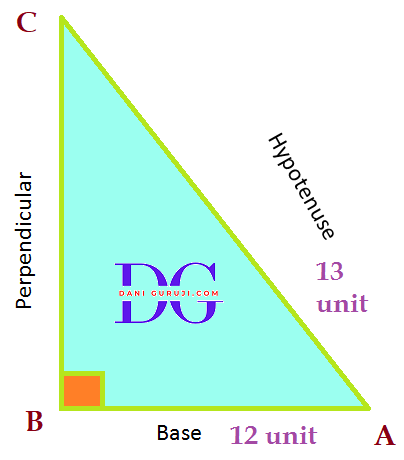
Pythagoras Theorem
According to Pythagoras Theorem, In a right angled triangle
(Hypotenuse) 2 = (perpendicular) 2 + (base)2
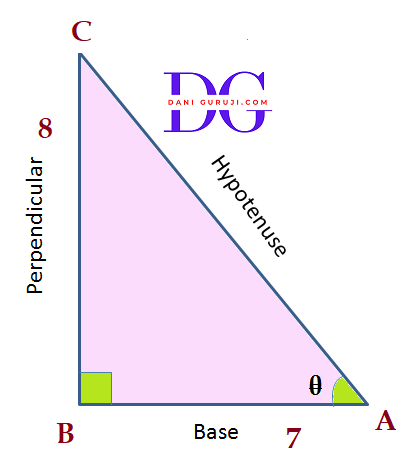
The trigonometric ratios
as per acute angle A and angle C in right triangle ABC are defined as follows-
| as per acute angle A |
as per acute angle C |
| Sine of ∠ A = $ Perpendicular \over Hypotenuse $ = BC / AC |
Sine of ∠ C = $ Perpendicular \over Hypotenuse $ = AB / AC |
| Cosine of ∠ A = $ Base \over Hypotenuse $ = AB / AC |
Cosine of ∠ C = $ Base \over Hypotenuse $ = BC/ AC |
| Tangent of ∠ A = $ Perpendicular \over Base $ = BC / AB |
Tangent of ∠ C = $ Perpendicular \over Base $ = AB / BC |
| Cosecant of ∠ A = $ Hypotenuse \over Perpendicular $ = AC / BC |
Cosecant of ∠ C = $ Hypotenuse \over Perpendicular $ = AC / AB |
| Secant of ∠ A = $ Hypotenuse \over Base $ = AC / AB |
Secant of ∠ C = $ Hypotenuse \over Base $ = AC / BC |
| Cotangent of ∠ A = $ Base \over Perpendicular $ = AB / BC |
Cotangent of ∠ C = $ Base \over Perpendicular $ = BC / AB |
|
|
|